Floyd Parte1

Floyd Parte2

Presentación #3

Definición, Pseudocodigo y Ejemplos del Algoritmo de Floyd-Warshall.

Floyd-Warshall

View more presentations from RickyTovar7.

Floyd-Warshall Demo

Reporte #5

Problema Lógico

Cajas de Fruta:

Estás en una isla y hay tres cajas de fruta que se han arrojado delante de ti. Una caja contiene solo manzanas, otra contiene únicamente naranjas y la otra caja contiene las dos, manzanas y naranjas.

Cada caja tiene una etiqueta una dice "manzanas", otra "naranjas", y otra "manzanas y naranjas". Usted sabe que NINGUNA de las cajas se han etiquetado correctamente - que están mal.

Si sólo se puede sacar y ver sólo una de las piezas de fruta de una sola de las cajas, ¿Cómo se puede saber el contenido real de las 3 cajas?

Solución:

Tomamos un pedazo de fruta de la caja de "Manzanas y Naranjas", Si se trata de una Manzana, entonces sabemos que es la caja de "Manzanas", ya que todas las cajas están MAL ETIQUETADAS. Esto significa que la caja MARCADA como "Manzanas" debe ser "Naranjas" y la caja MARCADA como "Naranjas" debe ser "Manzanas y Naranjas".

PROLOG

A continuación pondré el problema lógico anterior programado en Prolog, para ello use el Block de Notas para codificar los enunciados, y después los abría en Prolog para conocer la respuesta.

En esta primera prueba, estoy dando por echos, las 3 primeras lineas, le estoy asignando los valores del argumento de la prueba, y en la ultima linea pregunto, por decir así, si la "cajax" es de "manzanas" en alguna prueba.

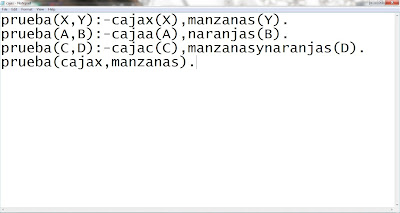
Este ya es el programa GNU Prolog y nos arroja el resultado "yes" en respuesta al código anterior, es decir, que SI es cierto o verdadero lo que preguntamos, que en este caso fue que si las "manzanas" pertenecian a la "cajax".

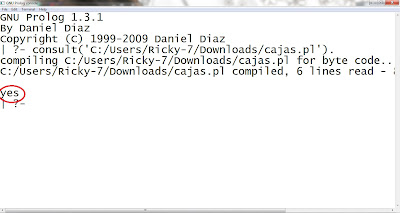
En este segundo ejemplo, las 3 primeras oraciones son las mismas, solo cambiamos la pregunta que si las "naranjas" pertenecen a la "cajac".

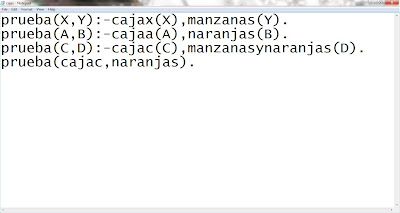
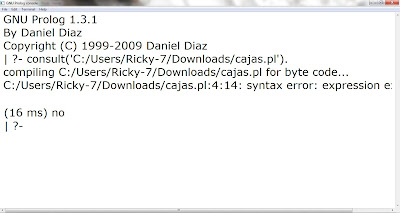
Y por lo tanto la respuesta es "no" ya que no pertenece la "cajac" a las "naranjas", en base a los hechos que pusimos. Por eso es una oración falsa.

Reporte #4

Lenguajes Funcionales

Los Lenguajes Funcionales son un paradigma de programación declarativa basado en el uso de funciones. Los programas escritos en estos lenguajes se componen solo por definición de funciones, entendiéndose como funciones puramente matemáticas.

Características:

• No hay asignación de variables.
• Carece de estructuras secuenciales o iteraciones.
• Todas las repeticiones de instrucciones se hacen por funciones recursivas.
• Se programa por medio de funciones.
• Carece de efectos laterales.

Un ejemplo de este tipo de lenguajes funcionales es el Dr.Scheme.

Dr. Scheme

Este lenguaje, forma parte de los Dialectos de Lisp, y facilita la programación funcional.

Características:

• Es un dialecto de Lisp.
• Tiene una sintaxis muy reducida.
• No necesita reglas de precedencia, ya que, carece de operadores.
• Una una notación prefija para todas las llamadas a una función.
• Permite la creación de procedimientos anónimos.
• Tiene un estándar minimalista, es decir, es fácil de escribir un compilador o interprete fiel a este estándar, que implementar uno en común con sus antecesores de Lisp.

Como Codificar en Dr.Scheme:

• Primero que nada se debe saber que todo va entre paréntesis.
• Se define el nombre de la función, a la cual sera llamada cada ves que se desee usar. Mediante la instrucción " (define(NOMBRE_DE_LA_FUNCION... "
• Se debe de tomar en cuenta que no debe haber espacios entre el nombre de la función.
• En la parte de arriba de la pantalla se crea la función, es decir, se generaliza para cualquier dato que ingresemos, y ne la parte de abajo, se aplica dicha función conforme a la función ya determinada, por medio de valores de entrada, dándonos enseguida el valor de salida de dicha función.
• Ver ejemplos.

Ejemplos:

Circunferencia de un Circulo

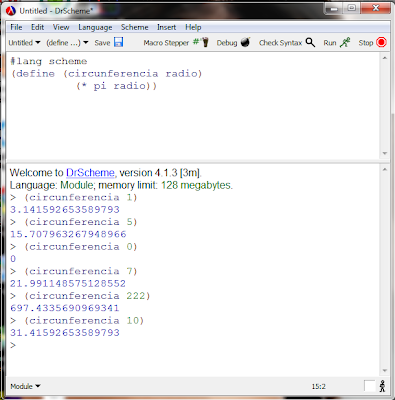
En este ejemplo, hice una función con la cual se pueda determinar la circunferencia de un circulo, a partir de un radio determinado. Se puede observar en la imagen que a la función llamada "circunferencia" se le asigna el valor de "pi" y al momento de usar la función solo se tiene que dar el valor del radio para el cual se desea saber su circunferencia.

Cuadrado de un Numero

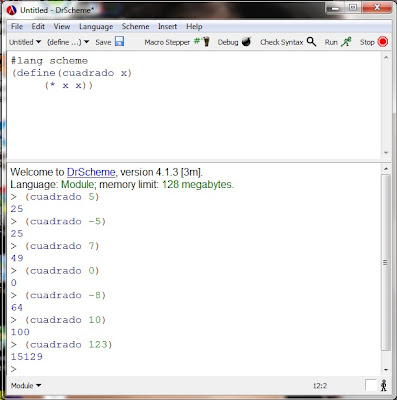
En esta función, se asigna un numero del cual queremos saber el cuadrado de ese numero, solo se llama a la función y se le ingresa el numero del cual saber su cuadrado.

Falso y Verdadero (True & False)

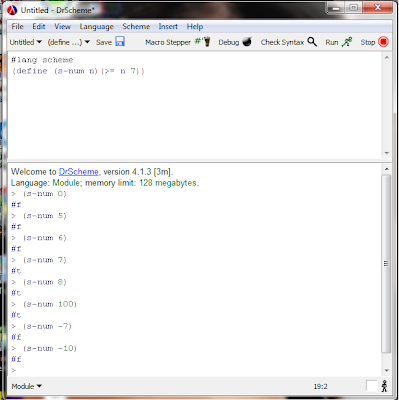
En esta función, se desea saber SI un numero dado es o NO es mayor o igual que un numero determinado en la función, por lo tanto al ingresar un numero queremos saber si es VERDADERO ó FALSO, entonces el resultado de salida sera "#f" para una respuesta "falsa" y "#t" para una respuesta "verdadera".

Números Positivos

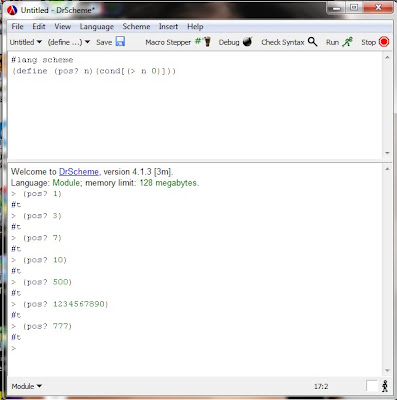
En esta función, se desea saber si un numero dado es positivo, y mediante una condición el programa nos arroja si lo es o no lo es.

Comparación de Números

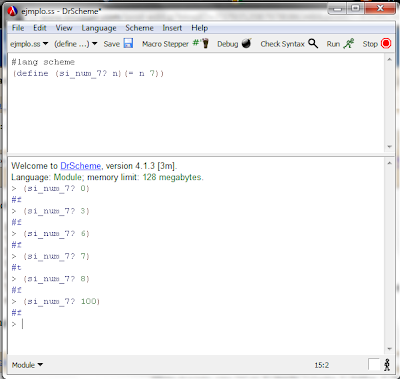
Esta función es muy especifica, ya que se desea saber si un numero es igual o no que otro, entonces solo habrá una sola respuesta correcta, es decir, solo el mismo numero puede ser igual a si mismo y por lo tanto todos los demás numero serán respuestas falsas.

Fuentes de Información

Tutorial

Descargar Dr.Scheme

Presentación #2

Quick Sort

Definición:

El ordenamiento rápido (Quicksort en inglés) es un algoritmo basado en la técnica de divide y vencerás, no solo nos sirve para organizar una lista de datos desorganizados, si no también, para optimizar el tiempo que se ocupa en realizar esta labor, ya que permite ordenar "n" elementos en un tiempo proporcional de O(n log n), lo cual es muy eficiente.

Funcionamiento:

Primero tenemos que elegir un elemento al azar al que llamaremos pivote.

Después de elegir el pivote analizaremos y empezaremos acomodarlos de tal manera que los elementos menores al pivote van del lado izquierdo y los mayores del derecho :

•elemento < pivote ="">

•elemento > pivote = Derecha

De esta forma obtendremos la posición del pivote elegido y a partir de ahí ordenaremos los demás elementos que del pivote se dividen en 2 sublistas las cual de igual manera elegimos un pivote y lo ordenamos como la primera ves y así sucesivamente se irán dividiendo en 2 sublistas pero cada ves menores lo haremos siempre que tenga mas de un elemento y después ya nos queda ordenada.

Ejemplos

Mejor y Peor Caso:

•En el mejor caso, el pivote termina en el centro de la lista, dividiéndola en dos sublistas de igual tamaño. En este caso, el orden de complejidad del algoritmo es O(n·log n).

•En el peor caso, el pivote termina en un extremo de la lista. El orden de complejidad del algoritmo es entonces de O(n²). El peor caso ocurre en listas que se encuentran ordenadas, o casi ordenadas. Pero principalmente depende del pivote, si por ejemplo el algoritmo implementado toma como pivote siempre el primer elemento del arreglo, y el arreglo que le pasamos está ordenado, siempre va a generar a su izquierda un arreglo vacío, lo que es ineficiente.

Pseudocódigo:

funcion quicksort(arreglo)

variables lista, menor, mayor, elemento

if longitud(arreglo) ≤ 1

return arreglo

else

//seleccionar un valor pivote en el arreglo

for each elemento en arreglo

if elemento < pivote entonces añadir “elemento” a menor

else añadir “elemento” a mayor

return concadenar_lista(quicksort(menor), pivot, quicksort(mayor))

Video